1楼到n楼的每层电梯门口都放着一颗钻石，钻石大小不一。你乘坐电梯从1楼到n楼，每层楼电梯门都会打开一次，只能拿一次钻石，问怎样才能拿到「最大」的一颗？

    如果把这题当作纯智力题,答案就是,第一层就拿钻石,以后每开一次门,发现更大就交换,否则do noting,这样到了100楼,怀中抱着的绝对就是最大的钻石,如果你还没累死的话.

    这种策略的思想本质是:万物皆备胎.

    但凡第一时间想出此类策略的人, 都应该面壁思过,且不说你们狡辩的交换不算拿.就单以道德层面来论,你们也不该这么干.你忘记你小时候梦想自己要当一个从一而终的人的决定了么!

    所以为了让大家找回从一而终的自己,重新扛起社会主义的大旗.我们必须严格地定义拿一次的限制,以正三观:钻石一旦拿起就无法放下了.(不要纠结于这些钻石为什么有这种能力,这不是重点- -.)

    so,这就变成了一个纯数学问题, 现在不再是怎样拿到最大的一颗,而是怎样以最大的概率拿到最大的一颗,这个概率又是多少?..........过程推导略, 直接上结果,结果是使用如下的策略可以有约37%的概率取到最大值:

    策略很简单,可以归纳为两点:

    1.先观察前k个钻石的大小

    2.从第k+1个开始一旦碰见最大的就停止

    然后根据简单的数学计算可以得出此策略模型下k的最佳取值为 k = n / e

    此时选中最大钻石的概率为p = 1 / e (约37%)

    下面是果壳网上关于该问题的计算机模拟10000次的统计结果.(n = 30的情况下)

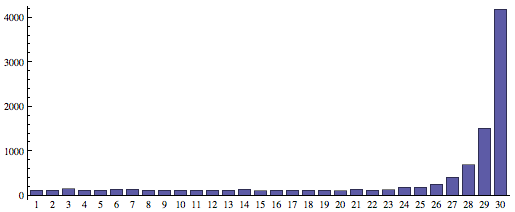
    可以看见该策略下,即使没选到最大值,选中次大值的概率也远远高于其他较小值,非常地具有现实意义.

灵活运用该结论,你将很有可能遭遇如下情景:

A:为什么,给我一个理由....你明明以前....

B:理由么,就是当年你给我的理由,我也一样

A:...

B:当年你跟我说我是那37%, 我后来查了好久才明白.

A:我后悔了

B:后悔木有开启备胎模式么?

A:...

B:你本来就有63%概率后悔的.

A:看来你已经习惯了这些冷冰冰的数字

B:拜你所赐

A:那我真的走了...再也不回来了...

B:无所谓,反正你是前面那37%

-----------------------

世界上最遥远的距离不是生与死,而是明明互为最优,却又互为前37%.

PS:如果想避免以上杯具发生,请各自将相关的n值定义为1,并且记得加上const 属性,严格防止被外部篡改- -!

参考链接:

wiki上此类问题的定义: 

变种取最大期望: